Brüche als Bruchzahl zeigen

Excel, alle Ver­sio­nen

Was bei der ersten Über­legung gar nicht so schw­er erscheint, ent­pup­PT sich rasch als irri­tieren­des Hin­der­nis: Brüche in Excel. Die Auf­gabe: Tra­gen Sie in A1 den Bruch ¹⁄₃ ein, im B1 einen beliebi­gen Mul­ti­p­lika­tor größer als 1 und berech­nen Sie in C1 das Ergeb­nis der Mul­ti­p­lika­tion mit =A1*B1 .

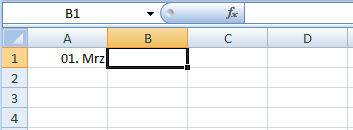
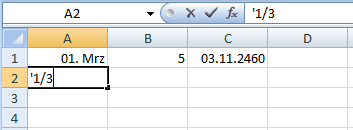
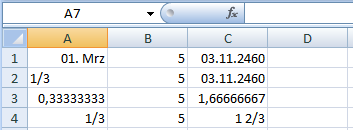
Die Ernüchterung kommt rasch. Geben Sie in A1 ganz nor­mal ¹⁄₃ ein, und Sie erhal­ten als Ergeb­nis sofort nach Ver­lassen der Zelle ein Datum, näm­lich den 1. März (des aktuellen Jahres):

Das Ergeb­nis ist erst ein­mal ein Datum

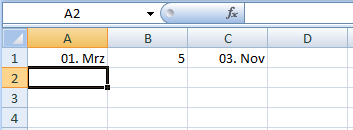
In der Erwartung (oder Hoff­nung), dass in A1 nur die Anzeige eine andere ist, fügen Sie in B1 eine 5 als Mul­ti­p­lika­tor ein und berech­nen in C1 das Pro­dukt:

Formeleingabe in C1 zur Berech­nung

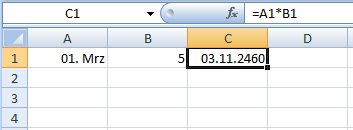
Wenn in A1 in Wirk­lichkeit ¹⁄₃ ste­ht (wie auch eingegeben), dann sollte das Ergeb­nis irgend­wie schlüs­sig sein. Aber Über­raschung:

Über­sachen­des Ergeb­nis der Berech­nung

Bei der Darstel­lung (sie ist Stan­dard) wird es Ihnen schw­er fall­en, eine Logik im Ergeb­nis zu find­en oder einen Bezug herzustellen. Aber wenn Sie C1 ein­mal anders for­matieren, wird Ihnen vielle­icht einiges klar­er:

Das Ganze ein­mal anders for­matiert

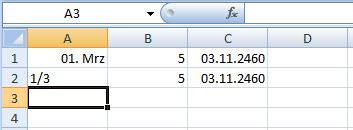
Der numerische Wert des 1. März (2012) wurde mit 5 mul­ti­pliziert und wiederum als Datum aus­gegeben. – OK, als erste Lösungsmöglichkeit wird Ihnen vielle­icht ein­fall­en, dass es ja den Trick mit der Eingabe als Text gibt. Dann ste­ht dort ja tat­säch­lich ¹⁄₃, nur links­bündig:

Die Bruchzahl als Text eingegeben

Gesagt, getan. Füllen Sie bitte auch B2 und C2 entsprechend aus. Na ja, der Men­sch denkt und Excel lenkt …

Auch hier das falsche Ergeb­nis

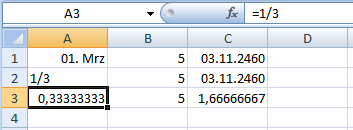
Was aber recht gut funk­tion­iert: Sie geben den Bruch als Formel ein, also =1/3. Das sähe dann so aus:

Als Gle­ichung eingegeben

Da wäre dann aber noch in A3 und C3 eine entsprechen­der For­matierung erforder­lich. Die wenig bekan­nte Lösung sieht so aus:

Eingabe als Bruch mit führen­der Null

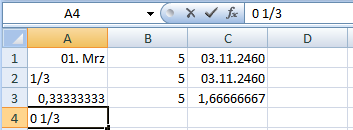
Sie geben in Spalte A eine Null, ein Leerze­ichen und dann den Bruch ein, also 0 ¹⁄₃. Spalte B und Spalte C füllen Sie wie gewohnt aus. Dann haben Sie sofort das kor­rekt for­matierte und natür­lich auch richtig berech­nete Ergeb­nis:

Das kor­rek­te Ergeb­nis

Und das Ganze funk­tion­iert natür­lich auch dann, wenn in Spalte B auch ein Bruch ste­ht. Die Logik, die dahin­ter ste­ht: Sie kön­nen ja in Excel direkt beispiel­sweise 5 ¹⁄₃ eingeben, also 5+1/3, um mit dem kor­rek­ten Wert weit­er zu rech­nen. Und wenn Sie statt der 5 eine Null ver­wen­den, dann bleibt natür­lich nur 0+1/3, also ¹⁄₃ übrig.

Die Basis dieser Zahlen mit dem einen oder anderen Beispiel mehr find­en Sie in dieser Datei.